牛顿迭代法

对于一元 N 次方程，当 N 大于 2 时没有固定的求根公式，为了求方程的根，可以使用牛顿迭代法。

牛顿迭代法的思想是在曲线上任意取一个点，然后求这一点的切线，使用切线的解来逼近多项式的解。

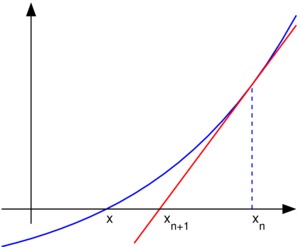
然后在 $x_{n+1}$ 处继续做切线：

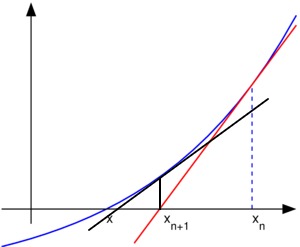
不断的逼近，可以看到上图中切线在 x 轴上的交点 $x_{n+1}$ 已与真实的解 $x_n$ 更近了一些。

这个过切点的直线的方程为：

\[y-f(x_n)=f^\prime(x_n)(x-x_n)\]

令 $y=0$ 可以求得 $x$，这里 $x_{n+1}$ 与 $x_n$ 的关系如下：

\[x_{n+1}=x_{n}-\frac{f(x_n)}{f^\prime(x_n)}\]

其中 $f^\prime(x_n)$ 表示 $f(x)$ 在 $x_n$ 处的斜率。

使用牛顿迭代法求平方根

求 $N$ 的平方根，可以理解为求如下函数的解：

\[f(x)=x^2-N\]

其中 $f(x)$ 的导数为：

\[f^\prime(x)=2*x\]

牛顿迭代式为：

\[x_{n+1}=x_n-\frac{x_{n}^2-N}{2*x_n}=\frac{1}{2}*(x_n+\frac{N}{x_n})\]

利用以上原理可以写出下面代码：

def sqrt(n):
    if n < 0:
        return float('nan')
    
    # 因为牛顿迭代法只是逼近真实值，所以需要设置一个误差范围
    e = 1e-15
    
    x = n
    x_next = (x + n / x) / 2
    
    # 两次迭代得到的解之间相差小于误差允许范围后跳出
    while abs(x_next - x) > e:
        x = x_next
        # 计算下一个近似解
        x_next = (x + n / x) / 2
    
    return x