快速排序
基本原理
快速排序是一种采用分治策略的排序算法,快速排序算法的流程如下:
- 从数组中任选一个元素作为主元(pivot)
- 把数组分成左右两部分,第一部分的元素都小于等于 pivot, 第二部分则都大于等于 pivot。
- 递归地对左右两部分采用上述算法。
把数组分为两部分,左边小右边大,然后对左右两边再做同样的划分,最终整个数组自然就有序了。
快速排序的基本过程如下:
void sort(vector<int>& nums, int lo, int hi) {
if (hi <= lo) return;
int i = partition(nums, lo, hi);
sort(nums, lo, i - 1);
sort(nums, i + 1, hi);
}
sort(nums, 0, nums.size());
其中最重要的是 partition 的实现,它原地对数组重排,并返回 i,保证重排后 nums[:i] <= nums[i:]。
partition 的实现
算法导论中提到了下面这种算法,选择区间中最后一个元素为主元。使用一个下标 i 指向最后一个排定的元素,然后在序列中寻找小于主元的元素,找到之后把它和 i 后面的元素交换位置,并更新 i。最后把主元放到 i 后面。
int partition(vector<int>& nums, int lo, int hi) {
int v = nums[hi-1];
int i = lo-1;
for(int j=lo;j<hi-1;j++){
if(nums[j] <= v){
i++;
swap(nums[i], nums[j]);
}
}
++i;
swap(nums[i], nums[hi-1]);
return i;
}
下面这种实现更为常见,也比较容易理解。它选择第一个元素作为主元,然后使用两个指针,从前向后寻找第一个大于主元的元素,并从后向前寻找小于主元的元素,然后交换两者。随后继续寻找,直到两个指针交叉为止。
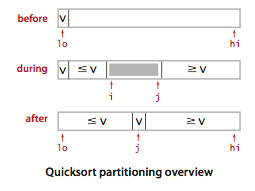
下面是一个例子,可以看到主循环退出后 j 指向值一定满足 nums[j] <= v,此时交换 nums[lo] 和 nums[j],划分就完成了。
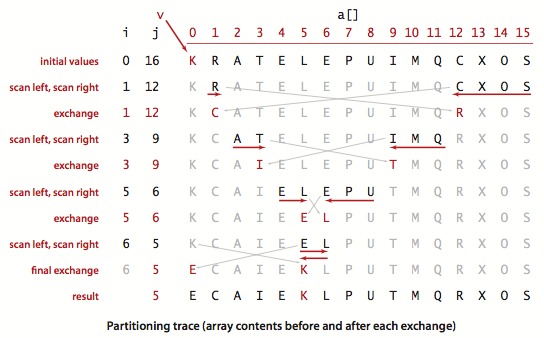
int partition(vector<int>& nums, int lo, int hi) {
int v = nums[lo];
int i = lo, j = hi;
for(true){
while(++i < hi && nums[i] < v);
while(--j > lo && nums[j] > v);
if(i >= j) break;
swap(nums[i], nums[j]);
}
swap(nums[lo], nums[j]);
return j
}
经过 partition 后,数组有如下特点:
nums[j]的位置就是它在最终排序好的数组中的位置。即,nums[j]已经排定。nums[lo:j]全都小于等于nums[j]。nums[j+1:hi]全都大于等于nums[j]。
上面的代码很简练,但是处处暗藏陷阱,能够准确无误地写出快速排序还是有些挑战的。
从 partition 函数中可以看到,初始时,i 和 j 都是指向超头超尾,在循环的一开始使用了 ++i 进行了自加。为什么不一开始就让 i 和 j 指向合适的位置呢?为什么不能写成下面这样呢?
// 这段代码存在错误
static int partition(vector<int>& nums, int lo, int hi) {
int v = nums[lo];
int i = lo +1;
int j = hi - 1;
while (true) {
while (i < hi && nums[i] < v) i++;
while (nums[j] > v) j--;
if (i >= j) break;
swap(nums[i], nums[j]);
}
swap(nums[lo], nums[j]);
return j;
}
考虑待排序数组:[1,1,2,3,4,5,1],这里 v=1,内部的两个循环结束的时候 i 指向第二个 1,j 指向最后一个 1,而后 swap 交换两者。下次循环结束时,i 和 j 的位置没有改变。于是就死循环了。
采用 ++i 和 --j 的写法,是为了避免这种情况,因为交换后的元素,下次一定会被跳过。
算法改进
预先将原数组打乱
最坏的情况下,原数组是完全倒序的,那么 partition 每次把数组的规模 -1。快速排序的时间复杂度退化到 O(n^2)。
为了避免这种情况,可以在排序前先把原数组打乱,如此就能避免出现最坏情况。
static void sort(vector<int>& nums) {
shuffle(nums);
sort(nums, 0, nums.size());
}
切换到插入排序
为了避免递归树的叶子太多,深度过深,可以对小的子数组采用插入排序,对于小数组快速排序比插入排序慢。
void sort(vector<int>& nums, int lo, int hi) {
if(hi <= lo + 10) {
Insertion.sort(nums, lo, hi);
return;
}
int i = partition(nums, lo, hi);
sort(nums, lo, i);
sort(nums, i + 1, hi);
}
三取样切分
快速排序中如果每次切分都能把数组均匀切分,此时能达到最高性能。选择数组的中位数作为 v 是最佳的。但是显然不能去遍历一下数组,找到中位数。一种方法是选择三个数,然后取这三个数中的中位数。
三取样切分策略是取数组中 lo hi mid 三个元素,经过比较后取中位数作为 v。同时可以将这个三个数的最大值放到 nums[hi] 的位置,这样可以保证内层的 while 循环不会越界,可以省去一个条件判断。
static int midian3(vector<int>& nums, int lo, int hi){
int mid = lo + (hi - lo) / 2;
if(nums[lo] > nums[hi]){
swap(nums[lo], nums[hi]);
}
if(nums[lo] > nums[mid]){
swap(nums[lo], nums[mid]);
}
if(nums[mid] > nums[hi]){
swap(nums[mid], nums[hi]);
}
return mid;
}
static int partition(vector<int>& nums, int lo, int hi) {
int mid = midian3(nums, lo, hi);
swap(nums[mid], nums[lo]);
int v = nums[lo];
int i = lo;
int j = hi;
while (true) {
while (nums[++i] < v);
while (nums[--j] > v);
if (i >= j) break;
swap(nums[i], nums[j]);
}
swap(nums[lo], nums[j]);
return j;
}
三向切分
如果数组中有大量重复元素,常规的快速排序中,会出现大量的交换相同元素的情况、三向切分的策略可以将数组分为三部分,小于 v 、等于 v、 大于 v,可以大幅加快快速排序的速度。
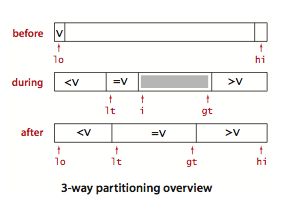
static void sort(vector<int>& nums) {
sort3way(nums, 0, nums.size());
}
static void sort3way(vector<int>& nums, int lo, int hi) {
if (hi <= lo) return;
int v = nums[lo];
int lt = lo, i = lo + 1, gt = hi;
while (i <= gt) {
if (nums[i] < v) {
swap(nums[i++], nums[lt++]);
} else if (nums[i] > v) {
swap(nums[i], nums[gt--]);
} else {
i++;
}
}
sort3way(nums, lo, lt);
sort3way(nums, gt + 1, hi);
}
除排序外的其他应用
假设现在要找出一个数组经过排序后下标为 k 的那个值。我们能否不对数组排序就找到它呢?有一种叫做 quick select 的算法,它能够轻松完成此任务。
其思路就是使用 partition。如果其划分点为 i,且 i == k,说明第 k 个元素已经排定了,nums[k] 此时的值和完全排序后 nums[k] 一致。
如果 i < k,说明前 i 个元素是最小的元素,可以设置 lo=i+1 再次划分。如果 i > k,说明 nums[i:] 间的元素是最大的 hi-i 个,可以设置 hi = i 再次划分。
如此不断地缩小范围,很快就能得到 i == k,此时就得到了结果。
static int select(vector<int>& nums, int k){
if(k >= nums.size() || k < 0){
throw out_of_range("index is out of range");
}
int lo = 0, hi = nums.size();
while(lo < hi){
int i = partition(nums, lo, hi);
if(i < k){
lo = i + 1;
}else if(i > k){
hi = i;
}else{
break;
}
}
return nums[k];
}
另外,一旦 nums[k] 已经排定,那么 nums[0:k] 之间的元素就一定是最小的 k 个元素,因此这个算法还可以用来寻找最小的 k 个数。