常见 CRT 预估模型总结
点击率预测模型的输入常常是高维稀疏稀疏向量,特征间的组合很重要,比如 “男生”、“游戏”、”晚间” 这三个特征的组合很可能触发点击行为,即男孩子在晚上没事干的时候喜欢玩玩游戏。点击率预测模型从 Logistics Regression 到 Factorization Machines,以及后来的神经网络模型,都在尝试高效地发掘组合特征。本文总结了近些年提出的 CRT 模型。
- FM (Factorization Machines)
- FFM (Field-aware Factorization Machines)
- Deep FM
- NFM (Neural Factorization Machines)
- AFM (Attentional Factorization Machines)
- DCN (Deep & Cross Network)
- Wide & Deep
- DIN (Deep Interest Network)
FM (Factorization Machines)
论文:Factorization Machines,这可以说是开创性的作品,但仔细想想,其实不复杂哈。后面提到的论文中,很多都是在这篇论文提出的模型的基础进行改进。
FM (Factorization Machine) 的思想是将组合特征的参数 $\mathbf{w}$ 进行矩阵分解,即 $\mathbf{w} = \mathbf{v}^T \mathbf{v}$。如此以来 $\mathbf{w}$ 可以由一个较小的句子 $\mathbf{v}$ 来表示。其中 $\mathbf{w}_{ij}=\mathbf{v}_i·\mathbf{v}_j$,即组合特征 $x_ix_j$ 的系数由为特征对应的隐向量 $\mathbf{v}_i$ 和 $\mathbf{v}_j$ 的内积。
FM 模型就可以表示为:
\[\hat{y}(\mathbf{x}) := w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j\]其中尖括号表示两个向量内积:
\[\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle :=\sum_{f=1}^{k} v_{i, f} \cdot v_{j, f}\]当数据很稀疏时,组合特征的参数难以学习到,FM 使用基于矩阵分解的策略,组合特征的系数依然能够有效估计,而且可泛化到未观察到的组合特征。
FFM (Field-aware Factorization Machines)
出自论文:Field-aware Factorization Machines for CTR Prediction
FM 模型的输入通常都是含有多个 Field 的稀疏向量,比如用户信息,商品信息,上下文信息,举例如下:
| Clicked | Publisher (P) | Advertiser (A) | Gender (G) |
|---|---|---|---|
| Yes | ESPN | Nike | Male |
FFM 认为不同类别的特征不应该向 FM 那样处在同一个隐空间中(FM 的所有特征的隐向量在一个特征空间中),FFM 把不同类别(每个 Field)区分在不同的特征空间中。
举个例子,当 ESPN 和 Nick 交互时,ESPN 要使用在 Advertiser Field 下 ESPN 的向量,因为 ESPN 在和广告商交互,而此时 Nike 要使用 Publisher Filed 下 Nick 的向量,因为此时 Nick 正在和发行方交互。
Deep FM
出自论文:DeepFM: A Factorization-Machine based Neural Network for CTR Prediction
模型结构如下:
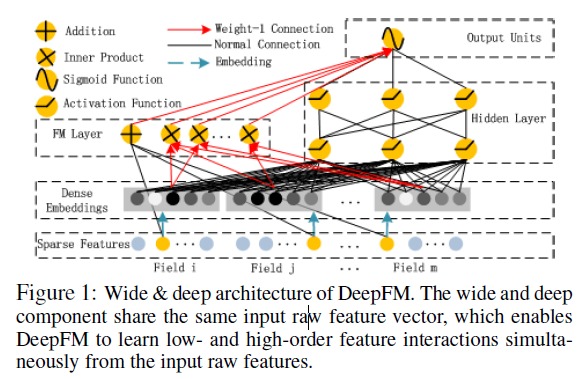
把 FM 和神经网络联合起来,FM 中各个特征有一个隐向量,Deep FM 把这些隐向量拼起来,输入给多层感知机(MLP),然后 FM 和 MLP 的输出加起来,作为最终分类。
FM 可以捕获到二阶特征,而 MLP 则能捕获到更高纬度的特征,将两者结合有望捕获更高复杂的组合特征。
NFM (Neural Factorization Machines)
出自论文:Neural Factorization Machines for Sparse Predictive Analytics
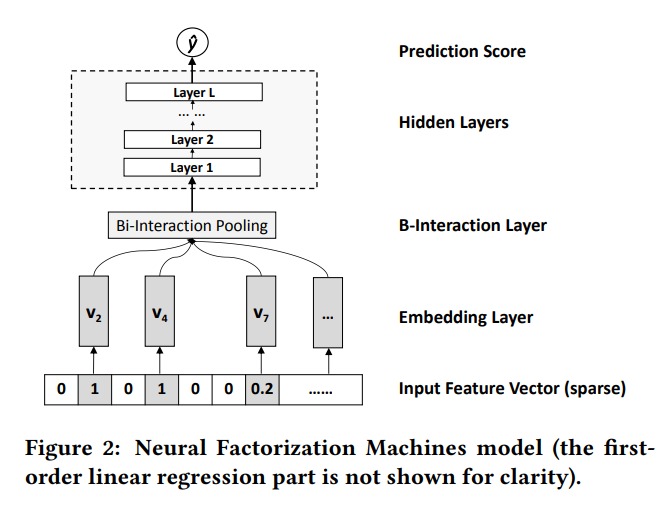
NFM 就是对 FM 的 cross 部分做了改进,不做点积,而是做对应元素相乘,最后加起来输入全连接层。
\[f_{B I}\left(\mathcal{V}_{x}\right)=\sum_{i=1}^{n} \sum_{j=i+1}^{n} x_{i} \mathbf{v}_{i} \odot x_{j} \mathbf{v}_{j}\]这玩意也能 work ?
AFM (Attentional Factorization Machines)
出自论文:Attentional Factorization Machines: Learning the Weight of Feature Interactions via Attention Networks
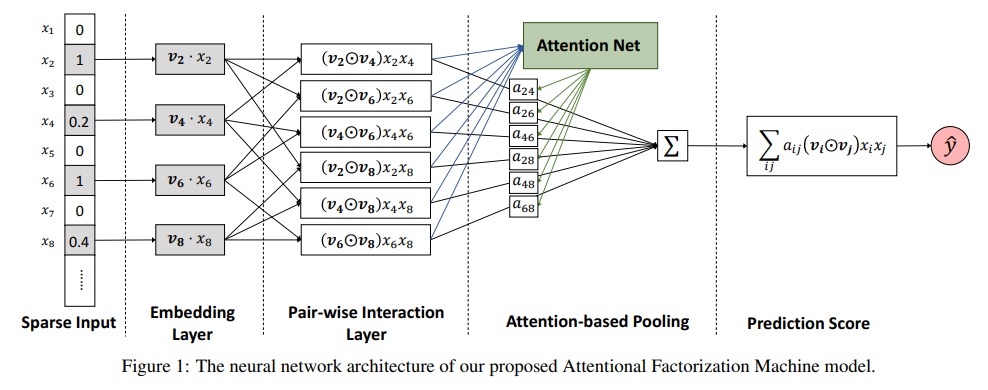
AFM 在 FM 的基础上引入了 Attention 机制,AFM 认为二阶特征不应该具有相同的权重,引入 attention 来增加权重。AFM 的模型如下:
\[ŷ_{AFM}(x)=ω_0+∑_{i=1}^{n}ω_{i}x_{i}+p^T∑^{n}_{i=1}∑^{n}_{j=i+1}a_{ij}(v_i⊙v_j)x_ix_j\]其中 attention 就是常见的感知机:
\[\acute{a_{ij}}=h^TReLU(W(v_i \odot v_j)x_ix_j+b)\] \[7 a_{ij}= \frac{exp(\acute{a_{ij}})}{ \sum exp(\acute{a_{ij}})}\]AFM 加入注意力机制,不同的交互特征使用不同权重,能够更有效地利用有用特征。
DCN (Deep & Cross Network)
模型的输入是稀疏的类别特征和稠密特征,category 特征经过嵌入得到稠密向量。将输入的稠密特征和嵌入得到的稠密特征全部拼接起来,得到向量 $x_0$。$x_0$ 分别输入到 cross network 和 deep network 中。两者的输出拼接后,交给全连接层进行预测。
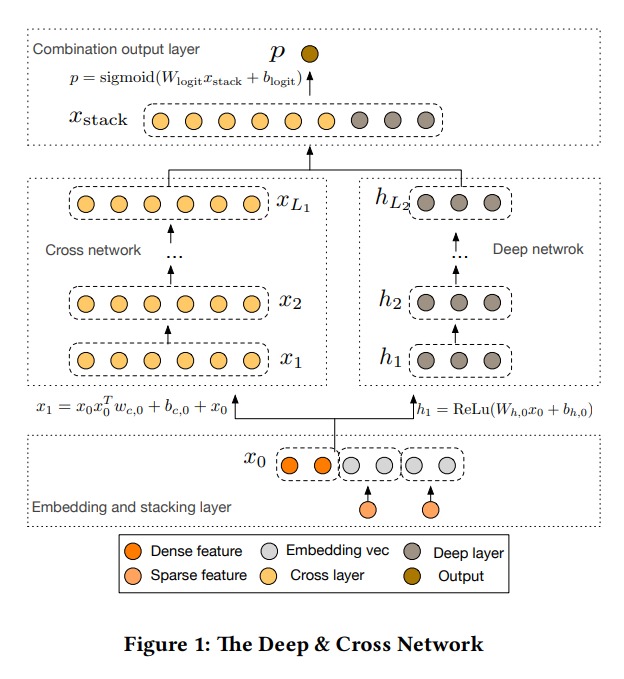
在 cross network 中,每一层的计算是下面这样的:
\[x_{l+1} = x_0 x_l^T w_l + b_l + x_l = f(x_l, w_l, b_l) + x_l\]向量计算的图形化表示如下:
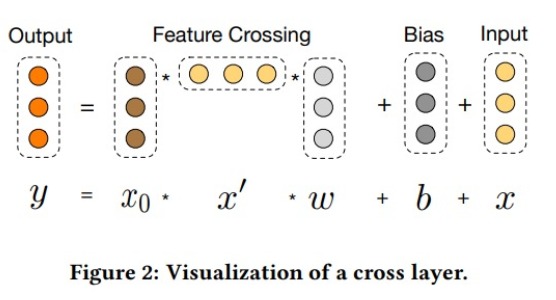
每一层的结果和原输入特征 $x_0$ 进行组合,就可以高效地组合出大量的高阶特征。
$x_0$ 和 $x^\prime$ 的乘积的结果是两个向量中各个特征两两组合的矩阵。这个矩阵中算是包含了所有的组合特征。但这个矩阵要乘以 $w$,而后矩阵中各列会加权求和得到一个向量。这样就把各种特征给加在了一起,组合特征混在一起,还能有意义吗?
这里的 $x_0$ 中包含特征 Embedding 的一部分,做 $x_0$ 各个维度的 cross ,好像还能捕获到到特征隐空间之间的关系。
在计算的时候有一点需要注意:
$x_0$ 和 $x^\prime$ 的乘积是一个矩阵,而 $x^\prime$ 和 $w$ 的乘积为向量,因此在计算的时候,应该先算 $x^\prime * w$,这样可以大幅节省时间和空间。
Wide & Deep
出自论文:Wide & Deep Learning for Recommender Systems
下图对比了 Wide & Deep 模型和单个的 Wide 和 Deep 模型。
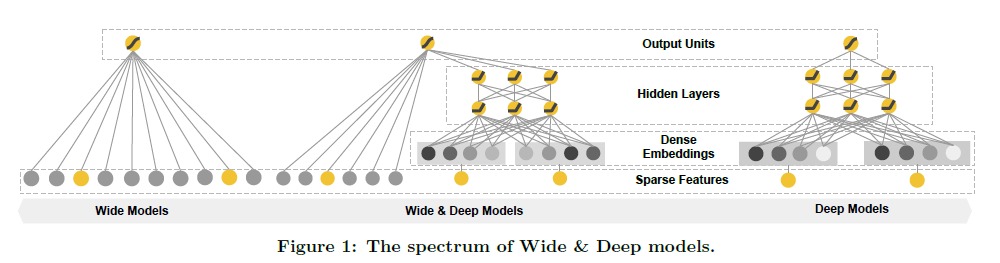
Wide 模型就是简单的线性模型,将稀疏的输入特征向量做加权和,而 Wide 部分是把特征做嵌入,然后拼接起来输入给多层感知机,最后 Wide 和 Deep 的输出加起来,作为整个模型的输出。
DIN (Deep Interest Network)
出自论文:Deep Interest Network for Click-Through Rate Prediction
DIN 的模型为下图中右边那个,左边的 base model 就是 wide & deep 中 deep 部分,DIN 在 deep 部分做了改进。
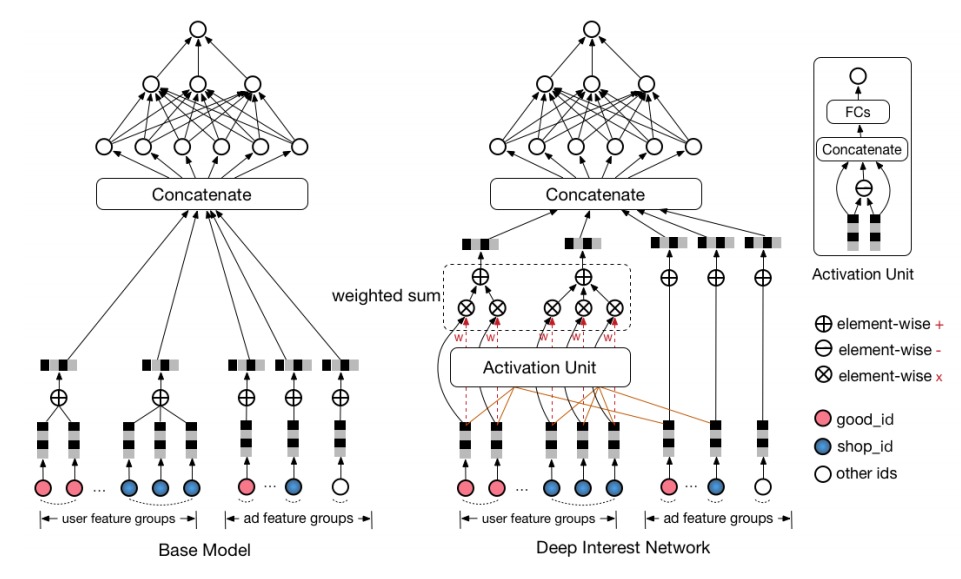
阿里巴巴提出的这个模型用于商品广告的排序,在进行排序的时候要用到用户的信息,这里就是用到用户的购买记录。包括用户买过的东西,买过东西的店铺,这些信息能够反映用户的偏好。但是对于待排序的 AD,并不是所有用户购买记录都有用。
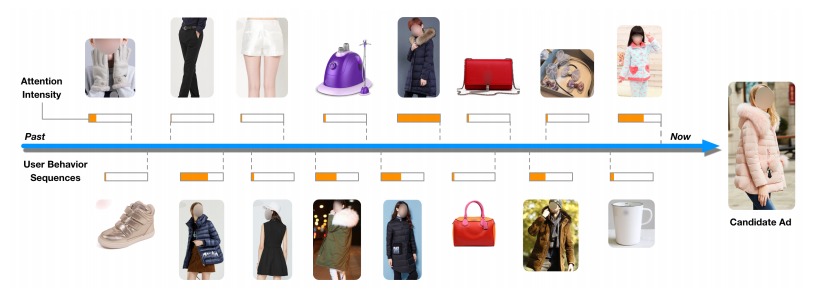
当计算衣服类的广告的 CTR 的时候,用户信息中最有用的就是用户曾经购买过的衣服的信息。所有这里使用 candidate 和 用户输入特征做了 attention。把用户购买的物品的特征使用 attention 的权重加权,把用户逛过的店铺的特征也加权起来。注意,candidate AD 是一个物品,它有自己所属店铺,在做 attention 的时候,那用户购买的物品和 candidate 做 attention,店铺和店铺做 attention。可以观察到,上图中不同物品算出来的 attention 是不同的,衣服的 attention 会更大一点,这就是 DIN 想要的效果。
模型图中的 Activation Unit 的输入是两个向量,输出的就是权重了。看起来好像上两个向量相减,再和两个向量拼接,然后输入全连接网络,得出权重。