论文阅读 - Factorization Machines
本文为阅读论文 Factorization Machines 时记下的笔记。
线性模型
线性模型,如 logistics regression 仅学习到输入特征的权重,无法利用组合特征。可以将特征彼此相乘,给线性模型引入非线性特征。如下式所示:
\[\hat{y}(x) := \underbrace {w_0 + \sum_{i=1}^{n} w_i x_i }_{\text{线性回归}} + \underbrace {\sum_{i=1}^{n} \sum_{j=i+1}^{n} w_{ij} x_i x_j}_{\text{交叉项(组合特征)}}\]如果输入特征 $x$ 的维度 $\vert x \vert = n$,整个模型的参数量为 $1 + n + n^2$。上式中交叉项 $x_ix_j$ 的系数 $w_{ij}$ 需要依赖特征 $x_i$ 和 $x_j$ 来训练得出。当输入向量 $x$ 很稀疏的时候。比如 $x$ 是使用 bag-of-word 表示的文档。当特征 $x_i$ 和 $x_j$ 没有同时出现时,$w_{ij}$ 就得不到训练。因此对于数据稀疏的场景,交叉项的参数矩阵 $\mathbf{w}$ 得不到充分训练。
FM
FM (Factorization Machine) 的思想是将组合特征的参数 $\mathbf{w}$ 进行矩阵分解,即 $\mathbf{w} = \mathbf{v}^T \mathbf{v}$。如此以来 $\mathbf{w}$ 可以由一个较小的句子 $\mathbf{v}$ 来表示。其中 $\mathbf{w}_{ij}=\mathbf{v}_i·\mathbf{v}_j$,即组合特征 $x_ix_j$ 的系数由为特征对应的隐向量 $\mathbf{v}_i$ 和 $\mathbf{v}_j$ 的内积。
FM 模型就可以表示为:
\[\hat{y}(\mathbf{x}) := w_0 + \sum_{i=1}^{n} w_i x_i + \sum_{i=1}^{n} \sum_{j=i+1}^{n} \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j\]其中尖括号表示两个向量内积:
\[\left\langle\mathbf{v}_{i}, \mathbf{v}_{j}\right\rangle :=\sum_{f=1}^{k} v_{i, f} \cdot v_{j, f}\]如果隐向量 $\mathbf{v}_i$ 的维度为 $k$,输入特征 $x$ 维度为 $n$,上面式子中第二项的时间复杂度是 $O(kn^2)$。不过这一项在计算的时候可以进行化简:
\[\sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j = \frac{1}{2} \sum_{f=1}^k \left(\left( \sum_{i=1}^n v_{i, f} x_i \right)^2 - \sum_{i=1}^n v_{i, f}^2 x_i^2 \right)\]下面是证明过程:
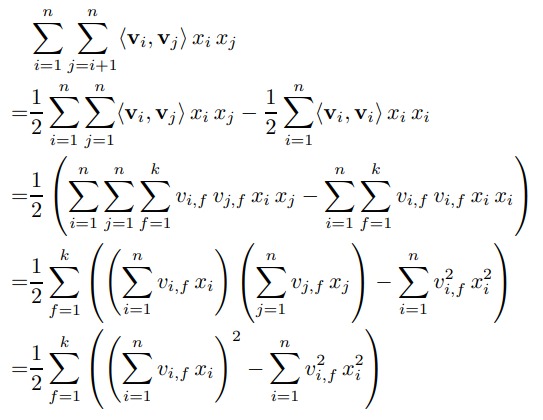
证明过程不难理解,注意下面几点:
- 第一步:注意第二个 $\sum$ 符号的起始值
- 第二步: 把向量内积展开成相乘并求和
- 第三步:提取公因式
- 第四步:改变符号得到 $\sum$ 的平方项
FM 特点
从参数量上来看,FM 模型将组合特征的参数量大幅下降,从 $n * (n-1) / 2$ 降到 $n * k$。
另外,采用类似于矩阵分解的策略,交叉项系数 $\mathbf{w}{ij}$ 原本只能通过 $x_i$ 和 $x_j$ 训练得出,如果这两个特征没有同时出现过,则得出的 $\mathbf{w}{ij}$ 无意义。在 FM 模型中 $\mathbf{w}_{ij}$ 由 $\mathbf{v}_i$ 和 $\mathbf{v}_j$ 内积得来,而 $\mathbf{v}_i$ 可以通过任何包含特征 $x_i$ 的实例进行学习。对于样本中不存在的特征组合,FM 也能进行泛化。
FM 训练
如果用 FM 做回归,可使用 MSE 作为损失函数。用于分类,就使用 logit loss,然后使用 SGD 训练即可。梯度计算如下:
\[\frac{\partial}{\partial \theta} \hat{y}(\mathbf{x})=\left\{\begin{array}{ll}{1,} & {\text { if } \theta \text { is } w_{0}} \\ {x_{i},} & {\text { if } \theta \text { is } w_{i}} \\ {x_{i} \sum_{j=1}^{n} v_{j, f} x_{j}-v_{i, f} x_{i}^{2},} & {\text { if } \theta \text { is } v_{i, f}}\end{array}\right.\]FM 和 SVMs 的比较
使用多项式核的 SVMs 的模型可以写成下面这样:
\[\begin{aligned} \hat{y}(\mathrm{x})=w_{0}+\sqrt{2} \sum_{i=1}^{n} w_{i} x_{i} &+\sum_{i=1}^{n} w_{i, i}^{(2)} x_{i}^{2} \\ &+\sqrt{2} \sum_{i=1}^{n} \sum_{j=i+1}^{n} w_{i, j}^{(2)} x_{i} x_{j} \end{aligned}\]这里 SVMs 和 FM 用到的特征完全一样,唯一的区别就是交叉项的系数。因为 SVMs 中交叉项系数 $\mathbf{w}_{ij}$ 依赖 $x_i$ 和 $x_j$ 学习出来,SVM 不能用在数据稀疏的场景下。而 FM 可以使用极度稀疏的数据来学习参数。
总结
当数据很稀疏时,组合特征的参数难以学习到,FM 使用基于矩阵分解的策略,组合特征的系数依然能够有效估计,而且可泛化到未观察到的组合特征。