论文阅读 - Matrix Factorization Techniques for Recommender Systems
本文为阅读 MF 经典论文 Matrix Factorization Techniques for Recommender Systems 的笔记。
推荐系统算法
从推荐系统做推荐的依据,大体上可以将推荐系统分为两种:
- 基于内容
- 协同过滤
基于内容的推荐算法
对于用户,根据个人身份信息或者回答相关问题,来构造用户的特征。对于物品,则根据物品自身的内容,或属性来构造特征。例如电影,其特征可以是类型、风格、参演演员等等。有了用户信息和物品信息之后,将两者特征向量化,然后用某种策略,来给各个用户匹配合适的物品。
基于内容的推荐系统,需要较多的领域知识。用户和物品的特征需要针对不同场景来选择和设计。
协同过滤推荐算法
协同过滤算法依赖于用户过去的行为信息,过去的购买记录、点赞记录、评分等等。协同过滤类的算法往往和领域无关,因为它不直接分析用户和物品自身的属性,只是基于用户与物品之间的交互信息(用户行为)来生成推荐。
协同过滤算法又可分为两大类:
1. Neighborhood methods
这类方法会寻找相似用户或相似物品,以相似关系为依据来生成推荐。包括 Item-based CF 和 User-based CF 两类。
2. Latent factor models
latent factor models 也基于 user-item 评分矩阵,但它并不用此矩阵来计算 user 或 item 间的相似度。而是用这个矩阵找出隐因素(factors),比如在电影推荐领域,喜剧、悲剧、动作、情感等都是会影响用户是否喜欢某特征。
latent factor models 通常采用矩阵分解的方法,将 user-item 评分矩阵分解为 user 和 item 矩阵。
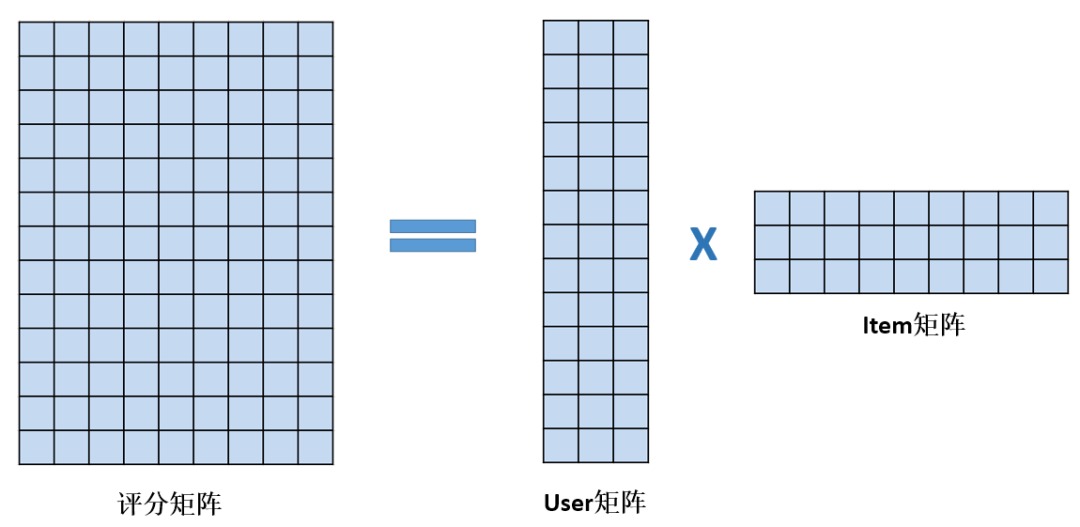
图片来自于 推荐系统之矩阵分解模型
user 矩阵的各行是 user 的向量表示 $p_u$,item 矩阵各列是 item 的向量表示 $q_i$。user 和 item 向量的每一维代表一种隐因子的强度。矩阵分解时可以控制 user 和 item 向量的维度,即控制隐因子的数量。
假如第一维代表的隐因子是电影的喜剧,那么 user 向量第一维的值表示该用户喜欢喜剧的程度,而 item 向量的第一维代表电影的喜剧成分的多少。
user 和 item 向量的內积就是 user 对 item 的评分,可以看出 user 和 item 向量越契合,即 item 的各种特征恰好是 user 喜欢的,那么评分就高。
\[\hat{r}_{u i}=q_{i}^{T} p_{u}\]矩阵分解
矩阵分解的策略有很多,常见的有 SVD (Singular Value Decomposition),NMF (Nonnegative Matrix Factorization) 等。
因为 user-item 矩阵往往是非常稀疏的,直接采用线性代数中的矩阵分解策略是行不通的。一种想法是利用矩阵中已有的值,期望 $q_{i}^{T} p_{u}$ 尽可能地接近这些值。得到 user 和 item 矩阵后,就可以恢复出完整的 user-item 评分矩阵,以此预测 user 对于没有评分过的 item 的评分。
这样以来矩阵分解可以转变成下面的优化问题:
\[\min _{q^* p^*} \sum_{(u, i) \in \mathbf{K}}\left(r_{u i}-q_{i}^{T} p_{u}\right)^{2}+\lambda\left(\left\|q_{i}\right\|^{2}+\left\|p_{u}\right\|^{2}\right) \tag{1}\label{1}\]对原评分矩阵中存在的值,希望 user 向量和 item 向量相乘后尽可能地接近该值。上式中另外加入了正则化项,防止过拟合。因为目的不单单是逼近 user-item 矩阵中存在的值,也希望能够最好地预测未知的数。
解上面的优化问题,可以使用随机梯度下降法,也可以使用交替最小二乘法。
随机梯度下降法(Stochastic gradient descent, SGD)
为了公式更短,先定义:
\[e_{u i}=r_{u i}-q_{i}^{T} p_{u}\]求偏导,即可得出更新公式:
\[\begin{array}{l}{q_{i} \leftarrow q_{i}+\gamma \cdot\left(e_{u i} \cdot p_{u}-\lambda \cdot q_{i}\right)} \\ {p_{u} \leftarrow p_{u}+\gamma \cdot\left(e_{u i} \cdot q_{i}-\lambda \cdot p_{u}\right)}\end{array}\]交替最小二乘法(Alternating least squares, ALS)
因为 $q_i$ 和 $p_u$ 都是未知的,前面的优化目标,公式 1 是非凸函数,不好求解。但是如果能够固定 $q_i$ 和 $p_u$ 中的一个,交替地更新另外一个,公式中只有一个变量,而且是二次的,优化问题就更容易得到最优解。
SGD 更容易实现且更快,但 ALS 可以并行化独立更新 $q_i$ 和 $p_u$。
优化策略
相较于简单的矩阵分解,作者提出了下面四点优化策略。
Adding biases
考虑到不同用户评分严格程度不同,打分范围不同。比如有的用户对很差的电影打 6 分,对好电影一律 10 分。而有的用户对差电影会打 1 分,好电影打分 9 分。这就是用户的偏差。
另外电影本身因为某种原因,也可以存在偏差,比如因为某些流量明星的加入,很烂的电影,也可以有 6 分。
因此可以将评分值分解为 4 部分:global average,item bias,user bias 和 user-item interaction。举个例子,已知所有电影的平均评分是 3.7 分,而 Titanic 是不错的电影,会比平均分高,其 item bias 为 +0.5,另外 Joe 是一个严格的人,一向打分就偏低,存在 user bias -0.3。因此 Joe 对 Titanic 的评分为:$3.7 + 0.5 - 0.3 + q^{T}p$。
考虑到上面这些因素,对评分的估计为:
\[\hat{r}_{u i}=\mu+b_{i}+b_{u}+q_{i}^{T} p_{u} \tag{2}\label{2}\]优化目标就变成了:
\[\begin{array}{l}{\min _{p^* , q^* , b^*} \sum_{(u, i) \in \mathrm{K}}\left(r_{u i}-\mu-b_{u}-b_{i}-p_{u}^{T} q_{i}\right)^{2}+\lambda} \\ {\left(\left\|p_{u}\right\|^{2}+\left\|q_{i}\right\|^{2}+b_{u}^{2}+b_{i}^{2}\right)}\end{array}\]对每个用户和物品学习一个偏置项。
Additional Input Sources
推荐系统往往需要处理冷启动问题,很多用户可能只对个别物品进行了评分,这就很难得出可靠的用户向量表示。引入其他的信息能够解决这种信息较少的问题。
推荐系统可以利用隐式信息,比如用户的浏览记录、搜索记录、鼠标停留信息等,在没有足够多的明确信息(购买、评分)时,此类信息也能在一定程度上对用户进行刻画。
考虑到上面这些,作者引入用户的 implicit feedback 和 user attributes 等信息。
implicit feedback 指的是浏览记录、搜索记录等。定义 $N(u)$ 为用户有过 implicit feedback 的 items 集合,每一个 item 对应一个向量 \(x_{i} \in R^{f}\) ,$N(u)$ 中的 items 给用户带来的特征可以表示为:
\[|N(u)|^{-0.5} \sum_{i \in N(u)} x_{i}\]前面的 $|N(u)|^{-0.5}$ 用于归一化。
另外用户自身的属性也是一个信息来源,设用户有一组特征 $A(u)$,每个特征用向量表示 $y_{a} \in \mathbb{R}^{f}$,用户的属性给用户来的特征可以表示为:
如此以来,用户对物品的评分可以表示为:
\[\hat{r}_{u i}=\mu+b_{i}+b_{u}+q_{i}^{T}\left[p_{u}+|N(u)|^{-0.5} \sum_{i \in N(u)} x_{i}+\sum_{a \in A(u)} y_{a}\right]\]和 $\eqref{2}$ 比起来,就相当于 $p_u$ 做了些调整。
Temporal dynamics
有很多因素会随时间变化,比如用户看的电影越来越多,眼光越来越刁钻,以前喜欢给电影打 4 星,现在倾向于打 3 星。引入时序信号,可以捕获到用户或物品随着时间的改变。
引入时序信号后,对 $\hat{r}$ 的估计变为:
\[\hat{r}_{u i}(t)=\mu+b_{i}(t)+b_{u}(t)+q_{i}^{T} p_{u}(t)\]$b_{i}(t)$ 是物品的 bias,它会随时间改变,比如电影刚上映时很好评如潮,后来人们越来越理智,评分渐渐变低。$b_{u}(t)$ 是用户偏置,如前面所述,用户的品味会变化。$p_{u}(t)$ 是用户向量,用户对各种电影的喜好会变化,比如之前喜欢看喜剧片,最近喜欢看惊悚片。$q_i$ 是隐因素向量,因为电影的各种因素相对稳定,因此不需要加时间因子。
加入了时间维度,式中 $b_{i}, b_{u}, p_{u}$ 就变成了和时间相关的变量了。是不是说它们在不同的时间就有不同的值呢?是不是将时间分段,每一段得到一组参数呢?详情可以参考文献1。
大体思路是,假设这些变量是随时间线性变化的,于是用一个线性模型来表示这些变量。线性模型 $y=at+b$,对每个变量学习一个斜率和截距,代入时间就可以得到对应时间的估计值了。
思考:
作者的这篇论文中的方法是用来评分预测的,Netflix 的比赛评估的是 RMSE,所以作者需要尽可能准确地预测缺失的值。加入时间信息,考虑到了用户品味等的变化。
这里是使用过去的部分信息,来预测过去的另一部分信息。但在实际的推荐系统中,需要用过去的数据预测未来的用户的评分。模型需要定期重新训练,以尽可能准确地预测用户在接下来的一端实际的评分。
Inputs With Varying confidence Levels
不是所有评分都有一样的权重,有些评分可能受到了广告的影响,这对刻画长期的特征贡献不大。因此,作者对每个观察到的评分引入了 confidence level,然置信度低的评分贡献小一点。如此,优化目标变为:
\[\begin{array}{l}{\min _{p^* , q^* , b^*} \sum_{(u, i) \in K} c_{u i}\left(r_{u i}-\mu-b_{u}-b_{i}\right.} \\ {\left.-p_{u}^{T} q_{i}\right)^{2}+\lambda\left(\left\|p_{u}\right\|^{2}+\left\|q_{i}\right\|^{2}\right.} \\ {\left.+b_{u}^{2}+b_{i}^{2}\right)}\end{array}\]实验结果
使用的数据是 Netflix 2006 年的比赛数据,作者获得了冠军,下图为上述几种算法的实验结果。图中曲线上的 50,100,200 表示 latent factor 横轴是模型参数量。根据纵轴的 RMSE 可以看出各种模型的性能。
总结
相比于最为基本的矩阵分解,本文考虑到了 bias,冷启动,特征随时间变化等事实,并将其融入到矩阵分解的策略中。本文是 Latent factor models 的经典之作,值得学习。
-
Y. Koren, “Collaborative Filtering with Temporal Dynamics,” Proc. 15th ACM SIGKDD Int’l Conf. Knowledge Discovery and Data Mining (KDD 09), ACM Press, 2009, pp. 447-455. ↩