论文阅读 - Neural Collaborative Filtering
这是本文要讨论的论文:

背景
在基于模型的协同过滤技术(Model-Based CF)中,矩阵分解(matrix factorization, MF) 应用的最多。在 MF 中 user-item 矩阵被分解为 user 矩阵和 item 矩阵。user 和 item 都被映射到一个隐空间中,各自有一个隐向量。这个隐向量可以用来做基于近邻的推荐(计算隐向量的相似度),也可以使用 user 和 item 隐向量的内积,来预测该 user 对该 item 的评分。
user 和 item 的隐向量内积,可以用来确定 user 对 item 的评分。有了 user 对各个 item 的评分,自然可以对 item 进行排序,得出推荐。但本篇论文认为,简单地使用隐向量内积,不足以捕获到复杂的交互行为特征,即评分并不一定是隐向量之积。本文通过引入神经网络,来学习用户与物品的隐向量和评分的关系。
问题设定
本论文讨论的是隐式反馈协同过滤场景,关于显示反馈和隐式反馈,定义如下:
- 显式反馈:直接反应出用户的喜好的行为,比如评分。
- 隐性反馈:间接反应用户的喜好的行为,比如浏览、点击、搜索
隐式反馈的数据由 0 和 1 组成,1 不一定表示喜好,0 只表示用户尚未和该物品有过交互。设 $Y$ 为 user-item 矩阵,则 $y_{ui}=1$ 表示 user u 和 item i 存在交互信息,否则 $y_{ui}=0$。
推荐问题就变成了预测矩阵中为 0 部分的评分,并以此来排序生成推荐。
Matrix Factorization,MF 分解 user-item 矩阵,将 user 和 item 映射到低位隐空间中,但 MF 存在一些问题,作者举了一个例子:
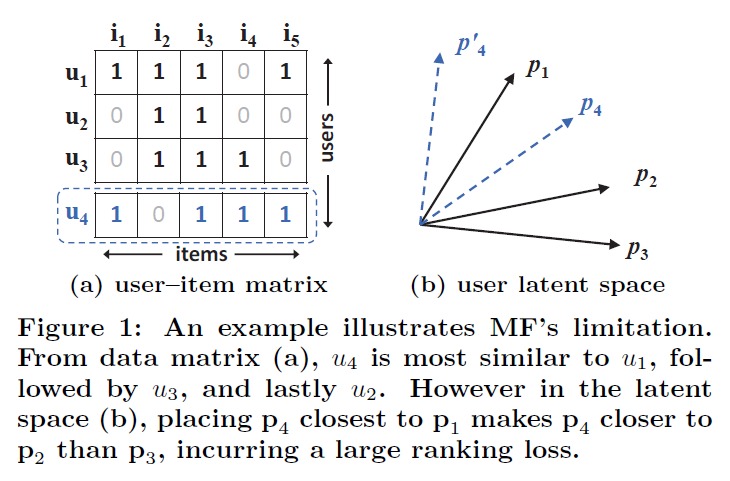
上图中,左边为原始的 user-item 矩阵,观察这个矩阵可以计算出,$u_1,u_2,u_3$ 之间的相似度。如果将矩阵进行分解,将 item 的向量降维至 2 维,$p_i$ 为 $u_i$ 的隐向量。右图中各向量的夹角可以正确地表达 $u_1,u_2,u_3$ 之间的相似度,$u_2$ 和 $u_3$ 最相似,$u_1$ 和 $u_2$ 的相似度大于和 $u_3$ 的相似度。
观察虚线框中的 $u_4$,它与 $u_1$ 最接近,其次是 $u_3$,最后才是 $u_2$。但在隐空间中,这种关系没法表示出来。$p_4$ 要想和 $p_1$ 的夹角最小,那么它必然和 $p_2$ 的夹角要小于和 $p_3$ 的夹角。
注:上面这个问题,直观地想,会在使用隐向量计算相似度的时候存在问题,因为相似度是用夹角衡量的。但怎么能说明 MF 使用内积来估计评分是有问题的呢?夹角大小关系在降维后出现了错乱,而 cosine 的分子上其实就是两个向量的内积。可能这能间接地说明,使用内积不足以可靠地预测评分。
Neural Collaborative Filtering
作者试图用一个模型来学习 user 和 item 的隐向量和评分之间的关系。下面是模型的基本结构,很容易理解。
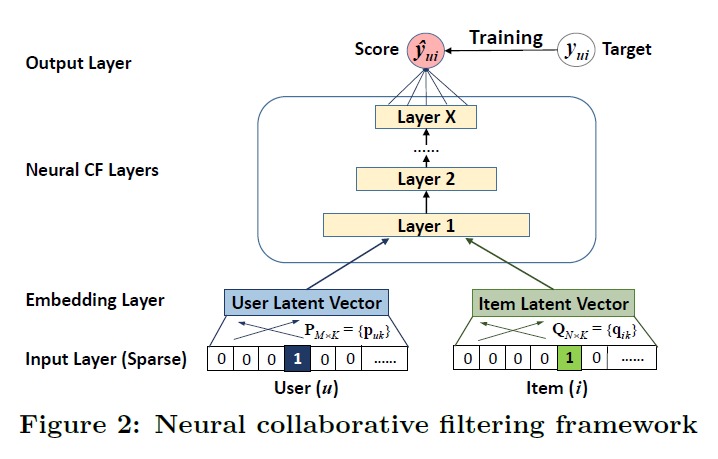
在 MF 中,其实就相当于对 user 和 item 做了嵌入,然后 user 和 item 的 Embedding 的内积等于 user 对 item 的打分,整体上可以作为一个回归问题,让均方误差最小即可。
而此处因为是隐式反馈,在 user-item 矩阵中,user 和 item 有交互就是 1,否则为 0。这里模型的输入为 user 和 item,当输入的 user item 对之间存在交互的时候,就希望模型输出 1,否则输出 0。
因此作者把问题转换为了一个分类问题,正例就是从存在交互的 user item 对,负例就是对每个 user 随机抽一些没有交互记录的 item,构成 user item 对,作为反例。
整个模型就是做一个二分类的任务,使用 log loss,用梯度下降训练即可。
Generalized Matrix Factorization (GMF)
作者指出如果上图中的 Neural CF Layers 部分做的工作就是将 user 和 item 的 Embedding 做点积(对应元素相乘),得到一个和 Embedding 等长的向量,然后交给 logistics regression。
\[\hat{y}_{u i}=a_{o u t}\left(\mathbf{h}^{T}\left(\mathbf{p}_{u} \odot \mathbf{q}_{i}\right)\right)\]上面式子中,$\odot$ 表示对应元素相乘,如果 $h$ 是全 1 向量,那模型实际上就是 MF 了。
Multi-Layer Perceptron (MLP)
既然都说了,MF 存在问题,那自然要改进了,改进方法就是引入多层感知机。把 user 和 item 的 Embedding 拼起来,然后输入给多层感知机,就可以了。这里的 Embedding 在 MF 的语境下,就是隐向量。
MLP 能够引入非线性的变换,有能力捕获到更加复杂的特征组合。有望利用 user 和 item 的隐向量,学得一个更好的模型,用以估计 user 和 item 是否存在交互。
结合 GMF 和 MLP
MF 对 user 和 item 的隐向量做内积,是线性模型。而 MLP 是非线性的。组合线性和非线性也许有效果,那就组合一下吧:
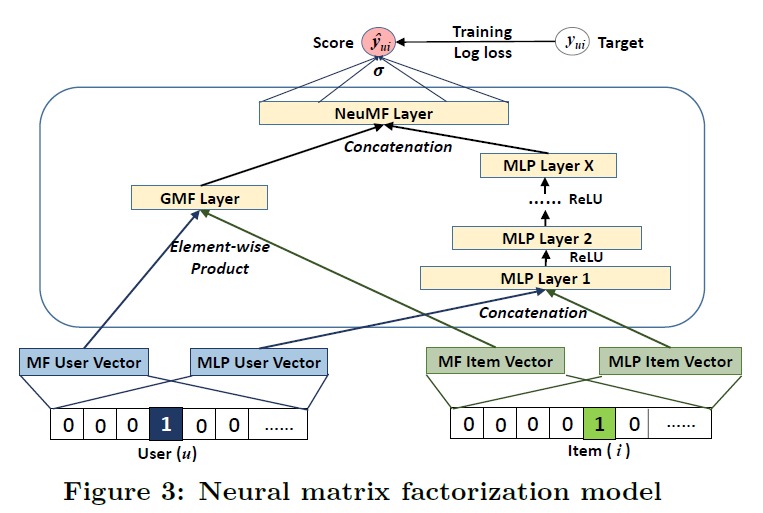
就是 MLP 和 GMF 的最后一层的向量拼接起来,然后交给 logistics regression。上图中好像 GMF 和 MLP 共用了一个 Embedding 一样。论文中说,共用 Embedding 需要 GMF 和 MLP 用相同的维度。学习单独的 Embedding 可能得到更好的集成效果。
实验
在训练的时候正样本就是由评分记录构造,针对每个 user 随机选取其未交互过的 item 来构造负样本。在训练时为每个 user 保留最近的一个交互过的 item,评估性能时,随机抽取 100 个未与用户交互的 item,并加入保留的 item。用训练好的模型对所有 item 进行排序,然后看保留的这个 item 出现的位置。位置越靠前,说明效果越好。
代码实现
论文原作者在 github 给出了实现:hexiangnan/neural_collaborative_filtering
我参考上面的实现进行了一些改写,专注于模型部分:NCF.ipynb