机器学习 - 主成分分析

在机器学习中，一个样本常常有多个属性，即多个维度。但不同维度间可能具有相关性，还有的维度则完全是噪声。主成分分析（Principle Component Analysis, PCA）找到样本中的线性无关的变量，样本的其他特征可以有这些线性无关的变量线性组合得来，这些线性无关的变量被称为主成分。

如下图所示，每个样本可以由坐标 $(x, y)$ 来唯一表示。但如果使用红色箭头表示的坐标系来表示，可以看到所有样本大都分布在其中一个坐标轴上，且样本两个坐标值之间没有了线性关系。

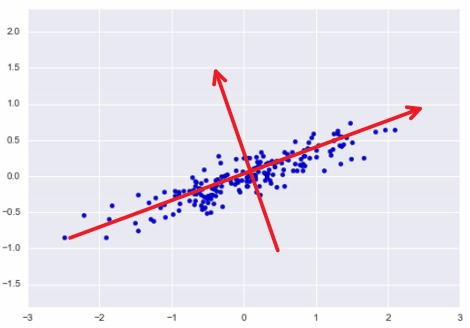
<width,500px>

所以如果将样本均投影到红色箭头表示坐标系下，每个样本就可以使用一个维度来表示，且不会损失太多信息。这就得到了降维的目的，由两维降到了一维。

PCA 将原本 $m$ 维的数据降维至 $d$ 维，相当于对原来 $m$ 维空间中的点投射到 $d$ 维空间中。

最大化方差

让样本在投射后的各个维度上应该分的足够开，即有较大的方差。

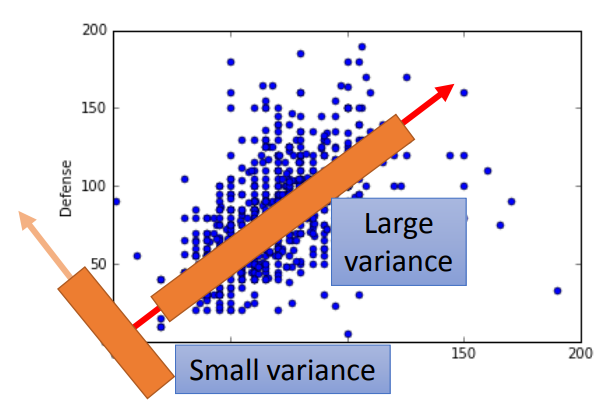
坐标变换，实际上就是对样本 $x$ 做一个线性变换，下图中， $x$ 是变换前的向量，$z$ 是变换后的向量。$z_1$ 就是 $x$ 在 $w^1$ 方向上的坐标。其中单位向量 $w^1$ 就是其中一个主成分的方向。

要保证在变换后，各个维度上有较大的方差，即 $var(z)$ 要越大越好。因为各个主成分相互正交，而且 $w^i$ 的模会影响方差值，所以这里限制 $W$ 为单位正交矩阵。

第一个主成分 $w^1$，就是能让 $var(z_1)$ 最大化，同时满足约束条件的向量 $w$。下图中蓝色方框中给出了具体式子和约束条件。

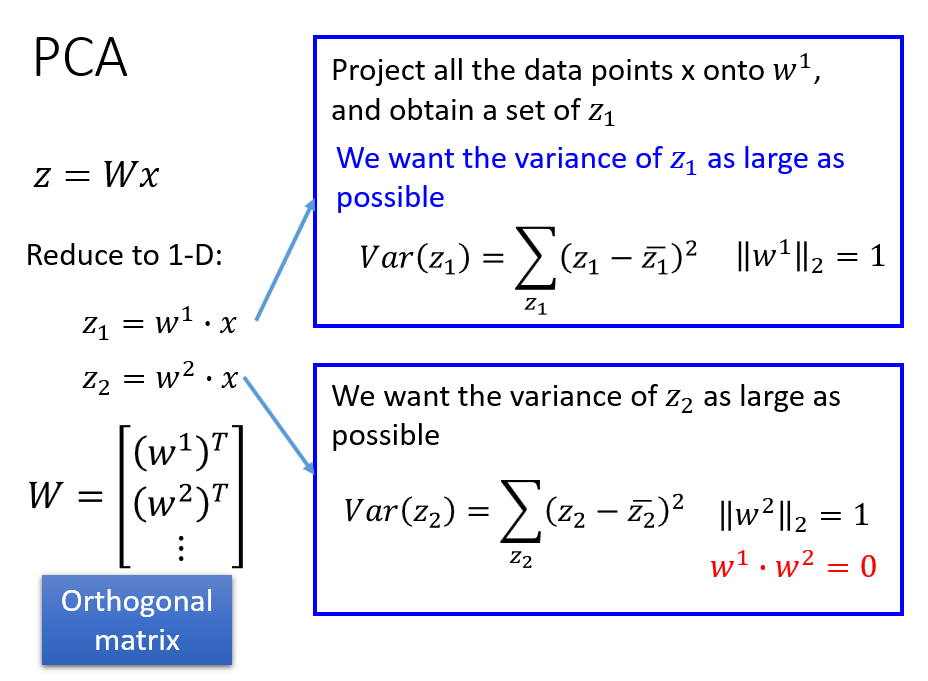
对方差 $var(z_1)$ 的进行化简：

在约束条件下求极值，使用拉格朗日乘子法：

可以看出:

\[\left(w^{1}\right)^{T} S w^{1}=\alpha\left(w^{1}\right)^{T} w^{1}=\alpha\]

要最大化 $\alpha$，就是让它等于 $S$ 的最大的特征值，这样以来 $w^1$ 就是 $S$ 最大特征值对应的特征向量。

相应地 $w^2$ 就是 S 第二大的特征值对应的特征向量。

因此，主成分就是 $x$ 的协方差矩阵的特征向量，主成分存在重要程度，由对应的特征值的大小决定。为了降维，通常选取最大的 N 个特征值对应的特征向量作为主成分。

最小化重建误差

从投射后的空间中恢复到原空间时，损失应该越小越好，即投射到新的空间下，没有损失太多信息。

要利用主成分重建原样本，一种方法是对主成分进行线性组合，就相当于拿主成分拼凑出原样本。另外一种方法是在所有样本的均值的基础上，加上主成分的线性组合，相当于在均值的基础上，进行修修补补得出原样本。

如果主成分具有很好的代表性，那么就能让重建误差足够小，因此可以定义损失函数：

这里 $u$ 为主成分，对于所有样本，找到一组 $u$ 让重建误差越小越好。

为了让误差足够小，即对每一个样本，可以用主成分 $u^i$ 以及一组系数 $c$ 让下面的等式两边足够接近。

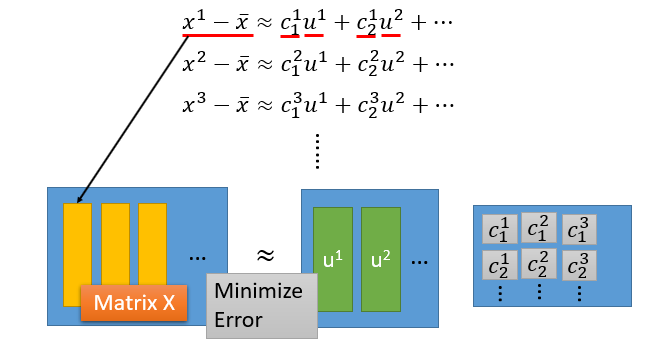
因为矩阵的 SVD 分解，可以保证分解后的矩阵相乘得到的结果和原矩阵相近，可以把矩阵 $X$ 写为 $X=U \Sigma V^{T}$ 。

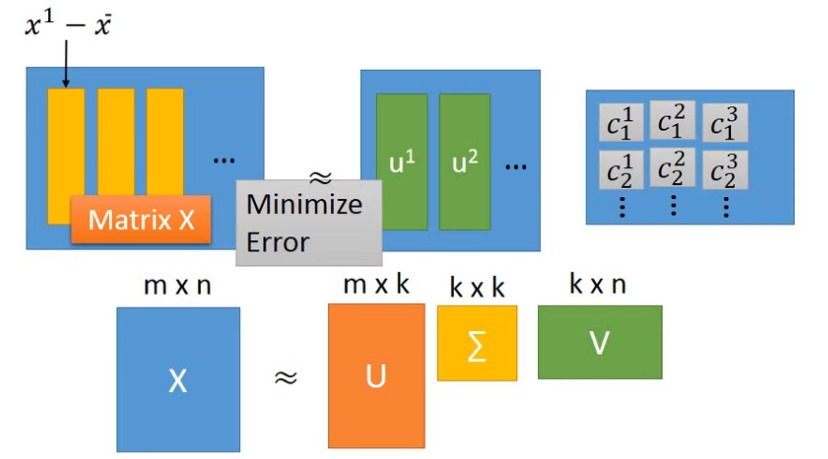
因此 $U$ 的各列就可以作为主成分，后面两个矩阵 $\Sigma$ 和 $V$ 的乘积就相当于系数矩阵 $C$。通过调整 SVD 分解时中间矩阵的维度，就可以得到不同数量的主成分。

因此做 PCA 降维的一种方法就是构造矩阵 X，然后对 X 做 SVD 分解，得到：

\[X=U \cdot \Sigma \cdot V^{T}\]

其中 $U$ 的各列为特征向量，$\Sigma$ 的主对角上为特征值。每个特征向量就是一个样本的基本组成成分，对应的特征值越大，该成分越重要。

实战

在 sklearn 中使用 PCA 的方式如下：

from sklearn.decomposition import PCA 

pca = PCA(n_components=2)
# pca = PCA(n_components=0.95)

X_pca = pca.fit_transform(X)

n_components 用于指定主成分个数。当取值为整数时，就是主成分个数。当取值为 0-1 之间的小数时，此小数指明了主成分包含信息量的占比。

在实践中，当样本量较少，特征中存在噪声时，使用 PCA 对数据降维，可以减缓过拟合。当数据量较大的时候，使用 PCA 往往会因为损失了信息，会导致训练效果变差。

"""
主成分
"""
>>> pca.components_
pca.components_
array([[-0.40711968, -0.5547244 , -0.70611078,  0.16715852],
       [ 0.1961092 , -0.0245544 ,  0.13603638,  0.97078956]])

"""
主成分方差所占比重
"""
>>> pca.explained_variance_ratio_
array([0.5655843 , 0.11474345, 0.10048613, 0.04653823])


"""
奇异值
"""
>>> pca.singular_values_
array([64.32040069, 41.74411226])

当样本量很大的时候，因为要进行矩阵分解，PCA 就会非常慢，为此可以使用 random PCA，它采用梯度下降的策略，寻找一个近似的矩阵分解方案。在样本量很大的时候，这个方法速度会快很多，且解的质量也不会太差。

pca = PCA(n_components=2, svd_solver="randomized")

WangYu's Notebook

机器学习 - 主成分分析

最大化方差

最小化重建误差

实战

推荐阅读