今天实验室的同学在面试中遇到了这样一个问题：写一个 sample(nums, k) 函数，从序列中等概率地抽取 k 个元素。

这个问题的解法，在《编程珠玑续》第 13 章有讲到。先前曾看到过，但有些忘记了，重新看书后，将解法梳理在此。

简单直白的解法

为了避免在后文中，因为下标导致的叙述不畅，我把这个问题改变一个说法：从 [1,n] 间的 n 个整数中取出 k 个元素，要求每个元素被取到的概率相等。

一个相当直接的解法如下：

import random

def sample(n, k):
    ret = set()
    
    for i in range(k):
        num = random.randint(1, n);
        while num in ret:
            num = random.randint(1, n);
        ret.add(num)
        
    return ret

注：random.randint(1, n) 返回 [1, n] 之间的整数。

这个算法每次随机产生一个数，然后检查之前是否之前已经出现过，如果已经存在了，就重新生成一个数。内循环 while 用来确保随机数不存在于 set 中。这个算法不够好，原因如下：

随机生成的数可能和先前生成的数重复了，这导致 while 循环可能会执行多次。当 k 远小于 n 的时候，随机生成的数与 set 中的数冲突的几率较小，这个算法的性能尚能接受。

但是当 k 接近 n 的时候，更极端一点，比如 n=k=100 时，在生成最后一个数时，while 会盲猜很多次，直到恰好碰到那一个不在集合中的数。如果随机数发生器不是完全随机，有可能永远不会生成 set 中缺失的那一个数，算法可能不会停止。

如果证明每个元素抽到的概率相同呢？这个过程其实相当于不放回的抽取，while 循环仅仅是模拟了不放回的事实。不放回的抽取，概率论老师已经告诉我们了，每个元素被抽到的概率是一样的。

Floyd 取样算法

在《编程珠玑续》上讲到了一种算法，这算法由 Bob Floyd 提出，可以保证在与 k 成正比的时间内得出结果，且保证等概率。代码如下：

def sample(n, k):
    if k == 0:
        return set()
    
    ret = sample(n-1, k-1)
    
    num = random.randint(1, n)
    if num not in ret:
        ret.add(num)
    else:
        ret.add(n)
        
    return ret

采用递归的思想，先从 [0, n-1] 中取出 k-1 个数，然后在 [0,n] 中随机生成一个数，因为目前集合中的元素一定属于范围 [0,n-1]，如果随机数和集合中的数冲突了，那就把 n 加入集合。这个算法保证每次生成随机数，都能得到一个可行元素。

但是它为什么有效呢？为什么能保证所有元素等概率被抽取到呢？下面证明每个元素被抽到的概率相等。

从 n 个数中取 k 个数，每个数被取到的概率为 $\frac{k}{n}$。考虑最后一次递归调用，从 [1,n] 生成的随机数 num=n 的概率为 $\frac{1}{n}$，有 $\frac{k-1}{n}$ 的概率为集合中已经存在的数。因此最后一次递归调用，向集合中加入的值为 n 的概率为:

\[\frac{1}{n} + \frac{k-1}{n} = \frac{k}{n}\]

考虑倒数倒数第 2 次递归调用，即抽取第 k-1 个数时。根据前面的分析不难得出 n-1 的概率为被加入集合的概率为 $\frac{k-1}{n-1}$。而最后一次递归调用中，在前一次 n-1 没被抽到的情况下，本次抽到 n-1 的概率为：$(1 - \frac{k-1}{n-1}) · \frac{1}{n}$。将前后两次递归中总的概率加起来，得：

\[(1 - \frac{k-1}{n-1}) · \frac{1}{n} + \frac{k-1}{n-1} = \frac{k}{n}\]

以此类推，可以证明每个元素被抽到的概率都是 $\frac{k}{n}$。

Floyd 非递归版本

写成递归形式的 Floyd 算法很容易理解，但为了更高的性能，可以去掉递归，用循环改写：

def sample(n, k):
    ret = set()

    for i in range(n-k+1, n+1):
        num = random.randint(1, i)
        
        if num not in result:
            ret.add(num)
        else:
            ret.add(i)

    return ret

测试

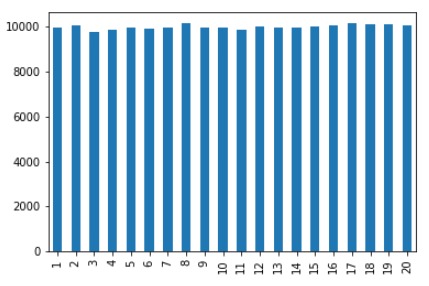
多次运行此取样算法，然后统计各个数被取到的频率，可以观察到所有数呈均匀分布。

counter = Counter();
for i in range(50000):
    random.seed(i)
    nums = sample(20, 4)
    counter.update(nums)

df = pd.DataFrame({"count": list(counter.values())}, index=counter.keys())
df = df.sort_index()
df.plot(kind="bar", legend=False)

蓄水池抽样

2020.1.3 补充：

今天在书上看到另外一种抽样方法，比起之前的方法更加简洁，而且我在 C++ 的 STL 中就发现了这种抽象算法的实现。

而且这个算法有一个巨大的优势，它能在只读的输入流中进行抽样，这意味中如果输入非常大，或者根本不知道会有多少输入的时候，此算法都能工作。

其思想是，先从输入流中取 k 个数，放到池子里，这个池子中保留的数，会在处理完所有数之后，作为抽样结果。对后续到来的第 i 个数，有 k/i 的概率用它替换池子中的一个数。这样每个数都有概率被选择，先出来的数由于 i 较小，因此被放入池子中的概率较大，但是因为它较早地被放入了池子，在后面被其他数替换的概率也会增大。该算法奇妙之处就是他能保证每个数被抽到的概率是相同的。

vector<int> sample(Stream<int>& stream, size_t k){
    srand(time(nullptr));
    vector<int> ret;
    int i = 0;
    // 先从流中拿出 k 个数放入池子中
    while(i < k){
        ret.push_back(stream.next());
        i++;
    }

    while(!stream.empty()){
        // 随机生成一个小于 i 的数，这里可能不严谨，但可以表达其中的意思
        size_t m = rand() % i;
        // m 小于 k 的概率就是 k / i
        if(m < k){
            // 替换池子中的数
            ret[m] = stream.next();
        }
        i++;
    }
    return ret;
}

证明起来很容易：

• 最后一个数，被抽中的概率为 $\frac{k}{n}$
• 倒数第二个数，在倒数第二次循环时被抽中的概率为 $\frac{k}{n-1}$，在最后一次被覆盖的概率为 $\frac{k}{n-1}· \frac{k}{n} · \frac{1}{k}$，把这两部分做减法能得到概率 $\frac{k}{n}$。