论文阅读 - Deep Neural Networks for YouTube Recommendations
本文为我在阅读 YouTube 工程师在 2016 年发表的推荐系统论文 Deep Neural Networks for YouTube Recommendations 时候记录的笔记。
前言
YouTube 是世界上最大是视频网站,在视频推荐系统的设计上,YouTube 面临以下挑战:
- 规模大:用户量与视频量都很大,要求算法能够适用于超大规模数据集。
- 更新快:每秒有小时级别的新视频上传,推荐系统需要对新视频及时作出反应,同时要处理好与已有视频间的平衡(不能光考虑新视频)。
- 噪声:用户的行为信息很稀疏,很少得到用户对视频是否满意的明确反馈。视频的信息结构化程度低。
系统概览
整个系统由 candidate generation 和 ranking 两部分组成,其中 candidate generation 从海量的视频中粗略地挑出几百个候选推荐视频,ranking 对这几百个视频做精细地排序,生成最终的推荐结果。
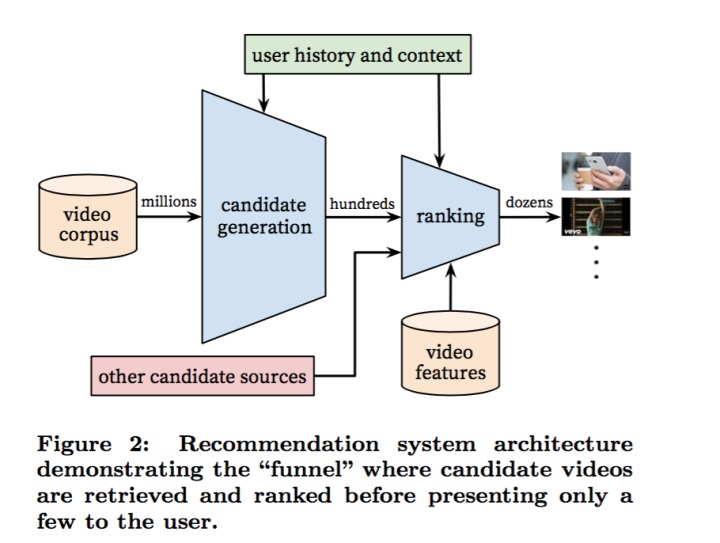
candidate generation 需要从百万量级的视频中快速地挑选出用户可能感兴趣的视频,因此其模型的开销要小,速度要足够快。ranking 阶段面对的是几百个候选视频,可以采用根据复杂的模型,利用更加丰富的信息。整个推荐系统采用了初筛+精选的策略。
CANDIDATE GENERATION
分类问题
candidate generation 目的是快速筛选出用户可能感兴趣的视频,这里 YouTube 的把寻找这些感兴趣的视频的问题,转为了一个多分类问题。直观的想,就是使用用户的浏览记录、搜索记录为输入,喜欢的视频为输出,来训练一个模型。有了这样一个模型后,下次单单输入用户的信息,就能预测出那些视频是用户所喜欢的。
用于分类的就是下面这个 softmax 模型,在视频库 $V$ 中,预测用户在时刻 $w_t$ 会观看的视频的 id。
\[P\left(w_{t}=i | U, C\right)=\frac{e^{v_{i} u}}{\sum_{j \in V} e^{v_{j} u}}\]其中 $u$ 为用户向量,$v_i$ 为视频向量。观察下一节中的模型结构就可以看出,$u$ 是神经网络最后一层的输出,而 $v_i$ 是 softmax 的参数矩阵中的第 $i$ 列。
模型架构
下图是 candidate generation 的模型结构图:
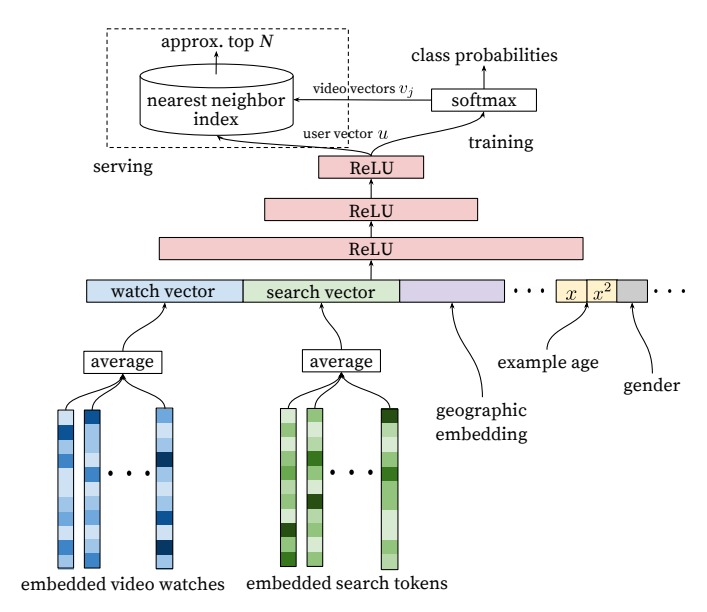
用户观看过视频通过嵌入并求评价得到了一个向量,搜索的文本也进行嵌入并求均值,加上其他一些用户信息,所有这些信息组合起来把用户被表示成一个向量,然后交给网络,模型的输出是对在几百万视频上的概率分布。
训练过程中,希望输出的概率分布中,希望用户观看过的视频的对应的维度概率最大。因为类别实在太多(几百万),这里采用了类似于 word2vec 中的训练思路,使用负采样。用户观看过的是视频为正例,负采样得到的样本做为反例。在训练过程中最小化正反例的交叉熵损失即可。(细节可以参考 word2vec 的那篇论文)
在线上时,并不使用 softmax,而是用用户的向量 $u$ 去查询最相似的视频。即计算 $u$ 和 $v_i$ 的內积,取內积最大的 $u_i$ 对应的视频作为初步筛选的结果。
特征
神经网络的优点之一(相比于矩阵分解),是可以很容易地把各种特征加入到网络中。对于每个视频都学到一个 embedding。用户的搜索词,切分为 unigram 和 bigram 后也进行嵌入。至于这里 embedding 是和整个模型一起联合训练得来的。
the embeddings are learned jointly with all other model parameters through normal gradient descent backpropagation updates.
example age
其中 example age 比较难理解,参考了别人的理解,大致描述如下:
这个 example age 是训练时刻减去训练样本产生的世界,即这个用户对某个视频的观看记录是在训练的前 10 分钟产生的,这个值可能就是 10,具体单位不详。
一个视频上传之后的一段时间里,其点击率是不同的,可能因为视频具有时效性,或者用户偏向于新视频等等。加入了这个时间的特征之后,模型就能够对视频在不同时刻的热度进行建模。比如一个视频在 10 天前热门,但在当下不热门了。或者如果十天前不热门,当前却很热门。这样 example age 可以正确地反映视频热度随时间的变化。在 serving 的时候,example age 设置为 0,就能够正确地反映该视频最新时刻的热度。
如果没有 example age 这一维度,那么模型对视频的热度的预测将是训练区间的平均值。
论文中放了下面这张图:
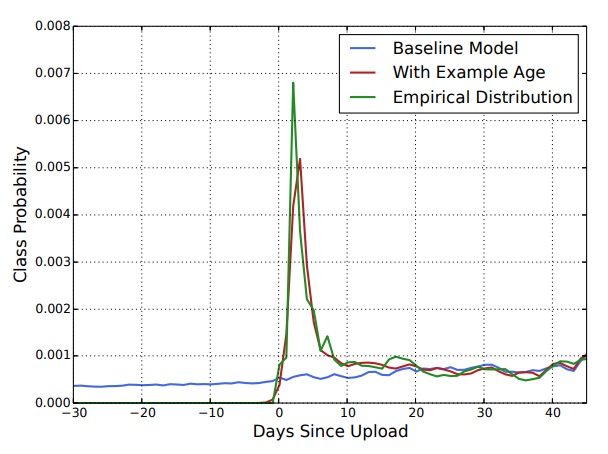
从这张图中可以看出,没有 example age 的时候,模型在各个时刻对某个视频的预测概率都差不对。但假如了这个特征后,不同时刻预测概率的有很大差异。即某个视频是在 0 时刻上传的。训练样本集中所有样本的世界分布在 -30 到 40 之间。在训练的时候,改变 example age 的取值,在 softmax 分类时,该视频的概率值有明显的差异。
图中指明 0 为上传时间,同时给出了一条绿色的曲线,这条线是经验分布(不知道时咋来的),大致指的是一个较好的概率分布。从图中可以看出,加入 example age 之后,对视频的预测概率在时间维度上的分布很符合经验值。
构造样本
监督学习需要有样本,这一节讲了在样本选择上的一些细节。
每个用户选择固定数量样本
为每个用户固定样本数量上限,平等的对待每个用户,可以避免少数活跃用户对模型造成巨大影响。
不考虑序列信息
用户观看记录,搜索记录都存在时间先后次序,这里去掉序列信息,对观看记录、搜索记录的 embedding 进行平均。
共同浏览的不对称性
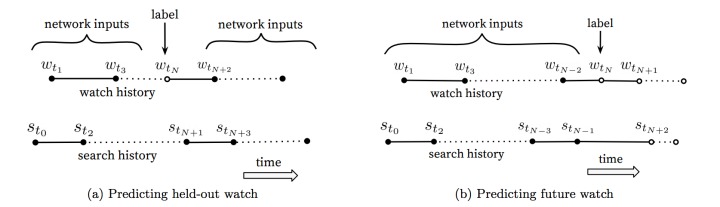
用户在浏览视频时候,常常是序列式的,比如按集观看。基于共现的思想,在这种情况下有一些特殊性,比如看了第一集很可能再看第二集,但看了第二集则鲜有可能再看第一集。
因此在选择训练样本的时候,图(a) 利用上下文信息预估中间的一个视频;图(b) 利用之前的所有信息,预估下一个视频。图(b) 的方式在 A/B test 中表现更佳。传统的协同过滤类的算法,都采用的图(a) 中的方式,没有考虑不对称的浏览模式。
RANKING
Ranking 的目的是使用更加丰富的信息对目标推荐对象进行排序,以及产生其他附带信息,比如视频推荐中生成缩略图。Ranking 也可以对多个来源的 candidate 进行集成。
Ranking 是对各个粗筛出来的视频进行评分,最终按评分排序,取评分最高的 N 个作为最终的推荐结果。
模型架构
Ranking 的模型和前面 candidate generation 大致相同,不同之处是最后使用了 weighted logistic regression。
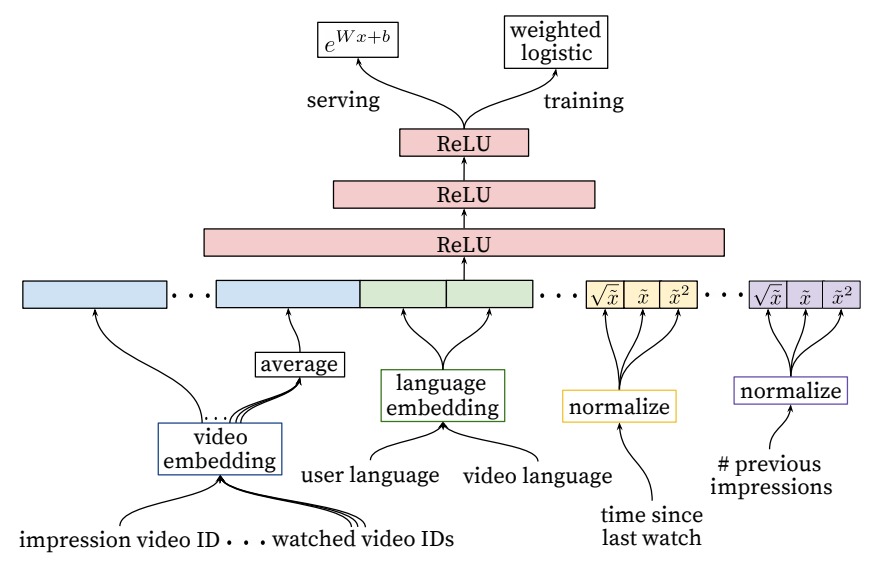
weighted 我的理解是在计算 loss 时加上权重。对于一个正样本,即用户观看过的视频,logistic regression 的输出应该越接近 1 越好。对于用户观看时间很长的样本,其 loss 应该更加重要,这里加权就是使用视频的观看时长进行加权。
特征
- impression video ID: 当前用于计算的 video
- watched video IDs: 用户观看过的最后 N 个视频
- language embedding: 用户语言和当前视频语言的 embedding
- time since last watch: 距上次观看相关视频的时间(统一个 channel,同一类型等)
- #previous impressions: 该视频已曝光给该用户的次数
前面两个 video id 都经过 embedding 层得到嵌入。观看过的视频的 embedding 做平均。time since last watch 可以反应用户看同类视频的间隔时间,假如用户某个 channel 的视频,那么他很可能会继续看这个 channel 的视频的,该特征就能很好的捕捉到这种用户行为。#previous impressions 则用于避免多次将同一个视频推荐给用户。上一次推荐后,用户没有点击,那么下一次就应该更换。
有几个特征还加入了 1/2 和 2 次项,这是为了给模型引入该特征的非线性变换。
期望观看时间
此处排序的依据是视频的期望观看时间,在 serving 阶段,并没有使用 logistics regression 输出概率值,而是使用了 $e^{Wx+b}$ 这样一个式子,下面稍作解释。
论文中提到了 odds 这个概念,在统计和概率理论中,一个事件的发生比(odds)是该事件发生和不发生的比率。
\[\begin{equation}odds(p) = \frac p{1 - p}\end{equation}\]而 logit 函数就是对 odds 取对数。
\[\begin{equation}logit(p) = log(\frac p{1 - p})\end{equation}\]Logistics Regression 就是用 $\theta^{T} x$ 去拟合 logit 函数:
\[logit(p)=\ln \left(\frac{p}{1-p}\right)=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2} = \theta^{T} x\]由此不难推出熟悉的 Logistics Regression 的式子:
\[p=\frac{1}{1+e^{-\theta^{T} x}}\]在本论文的 weighted logistics regression 中,正例会使用观看时间做加权,而反例的权重为 1。假设正例为 k 个,正例的观看时长为 $T_i$,共有 N 个样本,那么正例和反例的权重比为:
\[\frac{\sum T_{i}}{N-k}\]通常 odds 为即正例率比上反例率,而此处该模型的 odds 的期望就是上式。因为 k 往往相对 N 而言很小,上式近似于 $E(T)$,即视频的期望观看时间。
因此在 serving 的时候直接使用 $e^{Wx+b}$ 来计算出 odds,近似得到期望观看时间。
这一部分我觉得理解不够透彻,希望以后再遇到此类问题时,再次探究,或者和其他人交流
总结
阅读这篇论文,让我了解了这种 candidate generation + ranking 的推荐系统算法框架。本文中有很多工程上的技巧,感觉受用。比如分类类别极多的时候如何处理,在训练和 serving 的时候使用不同的策略来进行加速。另外加入 example age 以处理概念随着时间的变化,也相当巧妙。
对于我这刚刚开始探索推荐系统的菜鸟,要多多阅读此类经典的且优秀的论文,加油。